Mass-stream trajectories in binary systems

Oct 29, 2023

While working on my project on the role of disk mass-transfer in systems with main-sequence accretors I found that in many cases mass transfer occurred with a donor that rotated sub-synchronously (slower than the orbit), although the torques and other properties of the mass-transfer were calculated to occur from synchronous donors. It is important to properly account for this because my goal is to make a correct concensus of how important disk mass-transfer is in these systems, and using the wrong stream properties strongly affects whether disks will form.

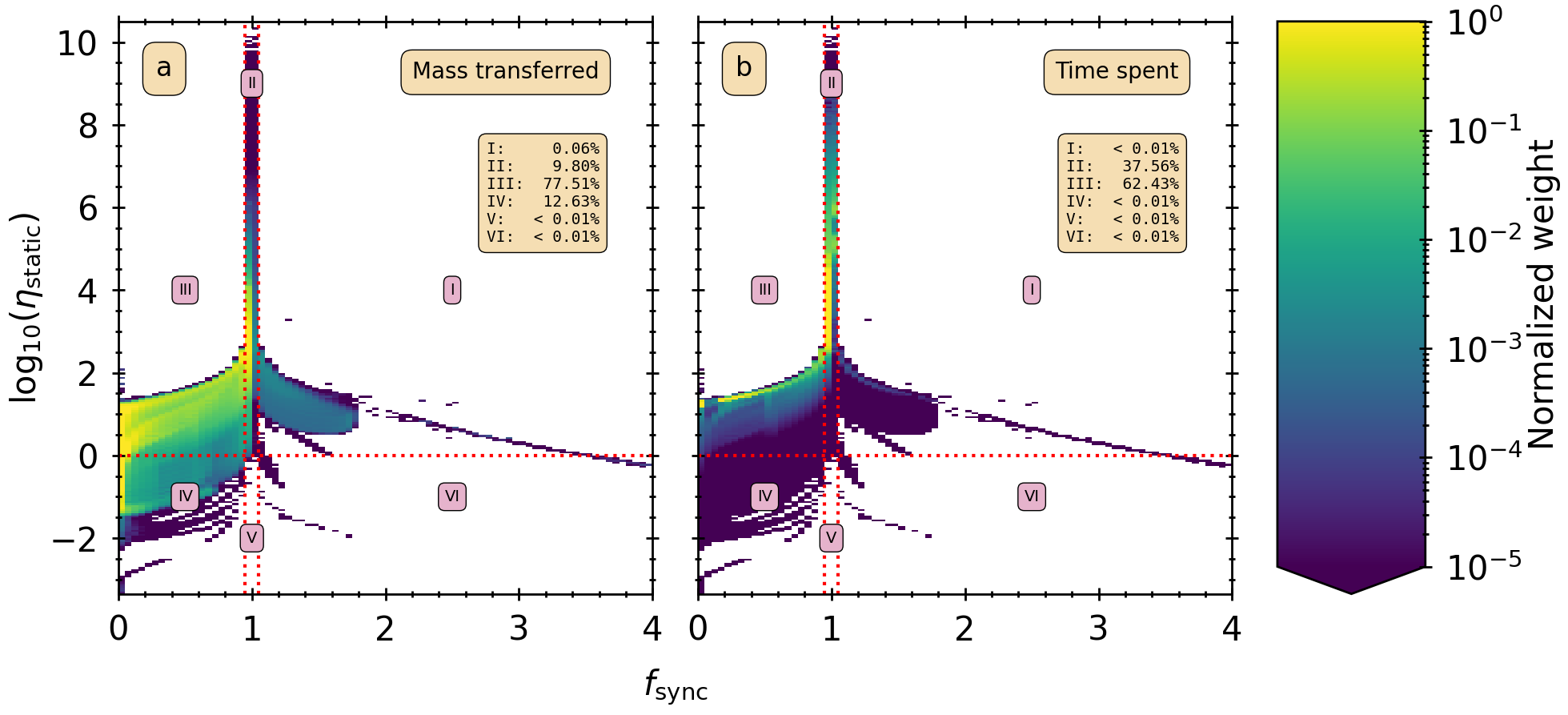
Figure 1: Synchronicity, fsync (abscissa, 1 is synchronous, below 1 is slower than orbital rotation, above 1 is faster) and how good the approximation of static tides is, log10(ηstatic) (ordinate, above 0 is approximately static, below 0 this approximation does not hold). In both the mass transferred as well as the majority of mass is transfered (given an entire population of binaries) in section III, sub-synchronous but with approximately static tides.
Figure 1: Synchronicity, fsync (abscissa, 1 is synchronous, below 1 is slower than orbital rotation, above 1 is faster) and how good the approximation of static tides is, log10(ηstatic) (ordinate, above 0 is approximately static, below 0 this approximation does not hold). In both the mass transferred as well as the majority of mass is transfered (given an entire population of binaries) in section III, sub-synchronous but with approximately static tides.

Finding that there was much asynchronous rotation prompted me to look deeper into this problem and see if I could implement something in binary_c to solve this issue. While other people have looked at this before, I culd find no publicly available datasets that contained the data to implement what I needed. At that point I decided to calculate this myself, and to make whatever results I found publicly available so other people can use this.

The project became a two-fold exercise:

  1. Evolve resolved binary system populations and track the relevant quantities:

    • relative velocity of the mass stream

      • mass-ratio of the binary system,

    • synchronicity of the donor,

      and we weigh these quantities by the amount of mass that is transferred with these quantities, and how much time is spent doing so

  2. Calculate ballistic trajectories of the mass-stream on a grid spanned by the above quantities.

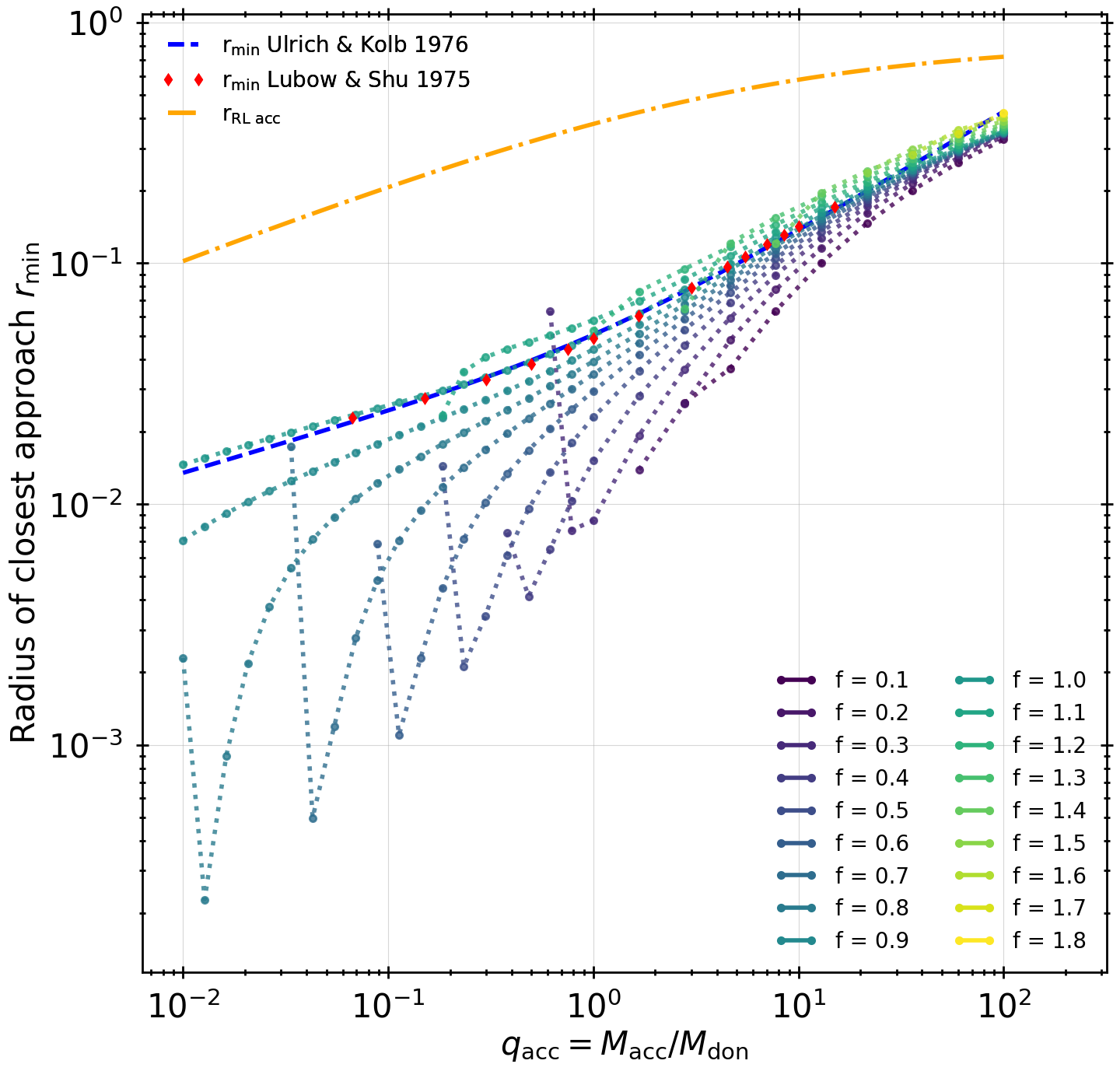
I wrote my own ballistic trajectory calculator (which I will make publicly available soon, I promise) and used this to calculate groups of mass-stream trajectories where I varied the mass-ratio, initial velocity and synchronicity factor of the stream. I calculated weighted averages of properties like the radius of closest approach, the angular momentum of the stream at that point and the angular momentum of the stream at certain fixed distances from the accretor.

In my paper I first introduce the topic of mass-transfer and asynchronously rotating donors, and go over the historical developments that came before my work. I then describe the equations of mass-stream trajectories and mass-transfer. In the first part of the result detail my findings of the binary populations which I use to motivate the rest of the study. The second part of the result section describes the results of two extremes: 1) asynchronous mass-transfer with slow and narrow streams and 2) aysnchronous mass-transfer with fast and wide streams. The discussion puts things back into a broader context and I conclude with some summarizing points of my findings.

Figure 2: Radii of closest approach for a grid of mass-ratios, qacc and synchronicity factors fsync. The red diamonds indicate the results of Lubow and Shu 1975 and the blue dashed line the fit on that data from Ulrich & Kolb 1976. Many stellar evolution codes use the prescription from Ulrich & Kolb. For perspective the orange dashed-dotted line indicates the Roche-lobe radius of the accretor.
Figure 2: Radii of closest approach for a grid of mass-ratios, qacc and synchronicity factors fsync. The red diamonds indicate the results of Lubow and Shu 1975 and the blue dashed line the fit on that data from Ulrich & Kolb 1976. Many stellar evolution codes use the prescription from Ulrich & Kolb. For perspective the orange dashed-dotted line indicates the Roche-lobe radius of the accretor.

The paper has now been published in MNRAS and is available on https://doi.org/10.1093/mnras/stad2077 and the pre-print is available on https://arxiv.org/abs/2307.04600. The data and routines to remake the figures in the paper are hosted on https://zenodo.org/doi/10.5281/zenodo.7007590.

David Hendriks
David Hendriks
Research Fellow Astrophysics

My research is on stellar astrophysics and the formation of compact objects, but I’m interested in many science related topics!