An important part of binary star interactions is the exchange of mass between the two stars. This mass exchange can lead to rapid rotation of the donor, or in certain cases the formation of a shared envelope of material that encompasses both stars. While this process of mass transfer has been studied extensively, some aspects of this are still working on some assumptions that may not always hold. The following post describes how I study one of these aspects, and how I try to relax some of the assumptions, potentially with large impact on how binaries actually interact.

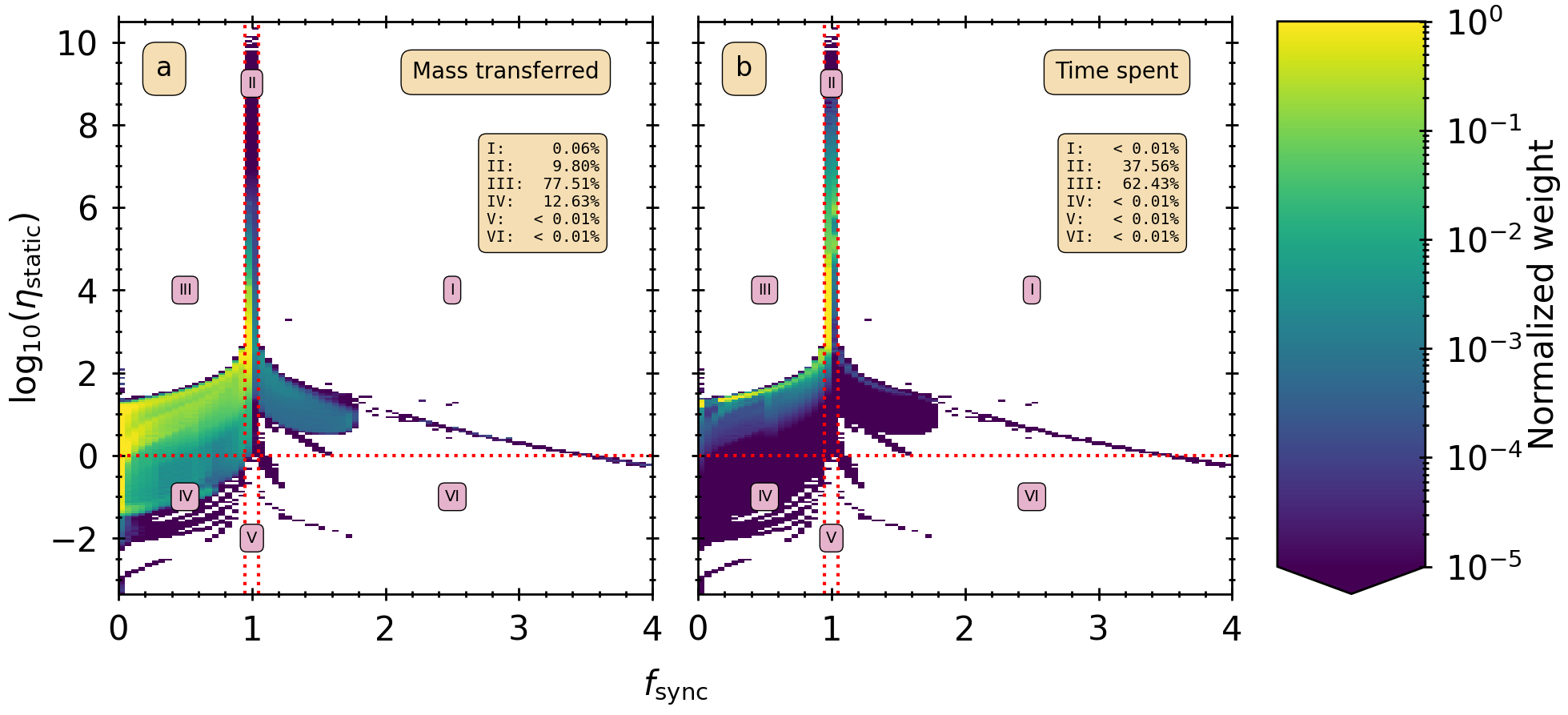
While working on my project on the role of disk mass-transfer in systems with main-sequence accretors I found that in many cases mass transfer occurred with a donor that rotated sub-synchronously (slower than the orbit), although the torques and other properties of the mass-transfer were calculated to occur from synchronous donors. It is important to properly account for this because my goal is to make a correct concensus of how important disk mass-transfer is in these systems, and using the wrong stream properties strongly affects whether disks will form.

Finding that there was much asynchronous rotation prompted me to look deeper into this problem and see if I could implement something in binary_c to solve this issue. While other people have looked at this before, I culd find no publicly available datasets that contained the data to implement what I needed. At that point I decided to calculate this myself, and to make whatever results I found publicly available so other people can use this.

The project became a two-fold exercise:

1. Evolve resolved binary system populations and track the relevant quantities:

   • relative velocity of the mass stream
   • mass-ratio of the binary system,
   • synchronicity of the donor

   and we weigh these quantities by the amount of mass that is transferred with these quantities, and how much time is spent doing so. This is to confirm that asynchronous rotation is actually relevant on a population scale, and with which system configuration this predominatly occurs.

2. Calculate ballistic trajectories of the mass-stream on a grid spanned by the above quantities.

   This is to provide the dataset to allow future projects to actually simulate the asynchronous mass transfer correctly.

I wrote my own ballistic trajectory calculator (available on https://gitlab.com/dhendriks/ballistic_integrator & https://gitlab.com/dhendriks/ballistic_integration, but beware this code is not cleaned up or made ready for public use) and used this to calculate groups of mass-stream trajectories where I varied the mass-ratio, initial velocity and synchronicity factor of the stream. I calculated weighted averages of properties like the radius of closest approach, the angular momentum of the stream at that point and the angular momentum of the stream at certain fixed distances from the accretor.

In my paper I first introduce the topic of mass-transfer and asynchronously rotating donors, and go over the historical developments that came before my work. I then describe the equations of mass-stream trajectories and mass-transfer. In the first part of the result detail my findings of the binary populations which I use to motivate the rest of the study. The second part of the result section describes the results of two extremes: 1) asynchronous mass-transfer with slow and narrow streams and 2) aysnchronous mass-transfer with fast and wide streams. The discussion puts things back into a broader context and I conclude with some summarizing points of my findings.

The paper has now been published in MNRAS and is available on https://doi.org/10.1093/mnras/stad2077 and the pre-print is available on https://arxiv.org/abs/2307.04600. The data and routines to remake the figures in the paper are hosted on https://zenodo.org/doi/10.5281/zenodo.7007590.

The dataset that is released with the paper contains two interpolation tables. The main interpolation table contains roughly 3 categories of data:

1. radius of closest approach of the stream and its associated circularisation radius (accretor accretion)

   This is to determine whether disk formation occurs or direct impact, and to calculate what the specific angmom of the disk is if so.

2. Specific angular momentum along the stream at fixed points (accretor accretion)

   This is calculated with the purpose of having a more correct torque on the accretor in the case of direct impact accretion, since the specific angular momentum of the stream evolves, it won't be the same as assuming it carries the same specific angmom as the circularisation radius. See Fig 6. in my paper https://arxiv.org/abs/2307.04600.

3. Initial and final specific angular momentum of the stream (donor accretion)

   This is to calculate the torque that the donor experiences when the stream accretes back onto the donor.

I am currently working on implementing this dataset in both a population synthesis framework (binary_c) to study how taking the effects of an asynchronously rotating donor on mass transfer on a population scale. This likely affects many types of post-interaction products like Algol systems, binaries with a stripped-envelope helium star, and double compact-object systems, but also systems like cataclysmic variables that are currently undergoing mass transfer. Moreover, following the Stable mass-transfer 2.0 workshop 2025 at the Flatiron Institute NYC USA, we are working on implementing these effects in the detailed stellar evolution code MESA as well. More on both of these efforts will be posted soon.